25 Mixed Strategy Equilibria; Infinite Horizon Games

For more information on these topics, see Allen, Doherty, Weigelt, and Mansfield Chapter 12: Game Theory.

In this chapter, we’ll finish up our unit on game theory by studying a couple more important topics.

25.1 Battle of the Sexes

The Battle of the Sexes is a game theory scenario about two people who want to spend time together but have different preferences for activities. In particular, the man prefers baseball and the woman prefers ballet.

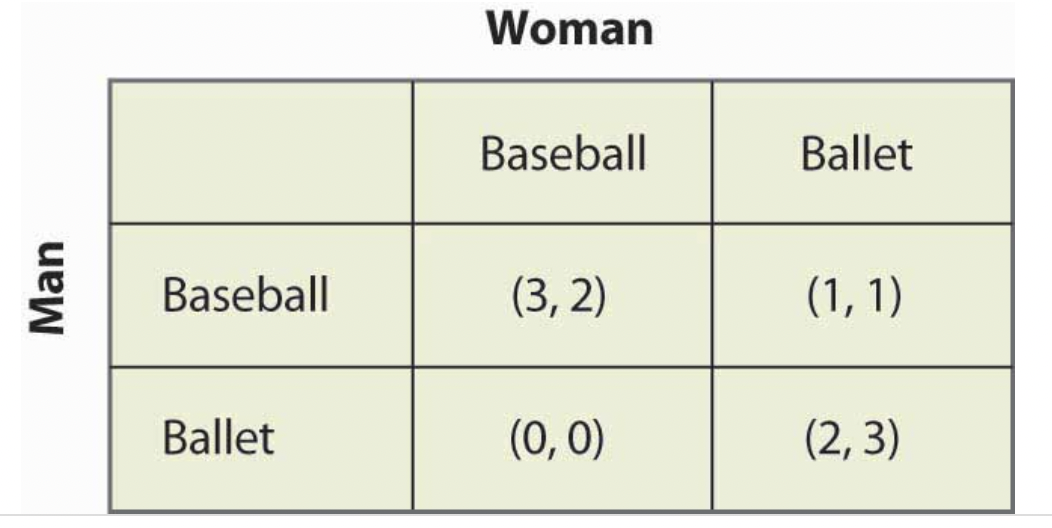
Classwork 1) Battle of the Sexes

Do players have a dominant strategy?
Find the (pure strategy) equilibria of the game.

There’s also a mixed strategy equilibrium of this game, where players randomize between strategies. For it to be a stable equilibrium, there must be no incentive for either player to change strategies. So if the woman picks baseball with probability (w.p.) 0.5 and she picks ballet w.p. 0.5, will the man also randomize between strategies? No, because he prefers baseball: if he picked baseball all the time, he’d get an expected payoff of $.5 (3) + .5 (1) = 2$, which is higher than if he also randomized with probabilities 0.5: $.25(3) + .25(1) + .25(0) + .25(2) = 1.5$.

The key to solving for the mixed strategy equilibrium, where the woman picks baseball w.p. $p$ and the man picks baseball w.p. $q$ is that $p$ must make the man indifferent between picking baseball and ballet, and $q$ must make the woman indifferent between picking baseball and ballet. Only then do we get a stable equilibrium. The math to solve:

Step 1: $p$ makes the man indifferent between picking baseball and ballet, so: E(man’s payoff from picking baseball given woman picks baseball w.p. p) = E(man’s payoff from picking ballet given woman picks baseball w.p. p):

\[\begin{align} 3p + 1 (1-p) &= 0p + 2(1-p)\\ 3p + 1 - p &= 2 - 2p\\ 2p + 1 &= -2p + 2\\ 4p &= 1\\ p &= \frac{1}{4} \end{align}\]

This makes sense: the man has a strong preference for baseball, so the woman must not pick baseball very often for the man to be indifferent between picking baseball and ballet.

Step 2: Now to solve for $q$: the value must make the woman indifferent between picking baseball and ballet, so: E(woman’s payoff from picking baseball given man picks baseball w.p. q) = E(woman’s payoff from picking ballet given man picks baseball w.p. q):

\[\begin{align} 2q + 0 (1-q) &= 1q + 3(1-q)\\ 2q &= q + 3 - 3q\\ 4q &= 3\\ q &= \frac{3}{4} \end{align}\]

This also makes sense: the man must pick baseball most of the time, because if he didn’t, the woman would pick ballet because she has a strong preference for ballet.

So the mixed strategy equilibrium here is that the man picks baseball w.p. 3/4 and the woman picks ballet w.p. 3/4.

Find the mixed strategy equilibrium of the battle of the sexes game when these are the outcomes and payoffs for (man, woman):
- (baseball, baseball): (4, 3)
- (baseball, ballet): (2, 2)
- (ballet, baseball): (0, 0)
- (ballet, ballet): (3, 4)

25.2 Infinite Horizon Games

We deal with games (or payoff streams) that may continue indefinitely using a discount factor $\delta$. The discount factor ($\delta$) helps us compare present and future payoffs in games that can go on indefinitely. For example, with $\delta = 0.9$:

A payoff of $1 today is worth $1
The same $1 payoff next period is worth $0.90 to you
The period after that, it’s worth $0.81
And so on…

For a stream paying $1 every period, the total value to you today is: \[1 + 0.9 + 0.9^2 + 0.9^3 + ...\] \[= \sum_{t = 0}^{\infty} 0.9^t = 10\]

To solve this sum:

Let $S = 1 + 0.9 + 0.9^2 + 0.9^3 + ...$
Then $0.9S = 0.9 + 0.9^2 + 0.9^3 + ...$
Notice that $S - 1 = 0.9 S$: subtracting the first term from S gives S multiplied by the discount factor.
Solve for S in the equation from number 3: $0.1 S = 1$, so $S = 10$.

This discount factor can represent either impatience: future payoffs are not worth as much to you as immediate payoffs, or the discount factor can represent risk: $\delta = 0.9$ means each period, there’s a 10% chance the game (and payoff stream) stops suddenly. Then the expected value of the payoff stream is $1 plus a 90% chance of getting a second dollar, plus an 81% chance of getting a third dollar, plus a 73% chance of getting a fourth dollar, etc: the payoff stream has an expected value of exactly $10.

Classwork 2) Discount Factors

Suppose you receive an infinite payoff stream of $1 each period, and your discount factor is 0.8. What is the total value of this payoff stream to you?
Suppose you receive an infinite payoff stream of $20 each period, and your discount factor is 0.95. What is the total value of this payoff stream to you?
Suppose you receive an infinite payoff stream of $50 each period, and your discount factor is 0.99. What is the total value of this payoff stream to you?
What represents a more patient person: a person with a discount factor of 0.9 or a person with a discount factor of 0.99?

Repeated Games

Repeated games represent situations where players interact multiple times over an extended period, which is common in business and personal relationships. Unlike one-shot games, repeated interactions allow for strategies based on trust, reputation, and reciprocity since players must consider both immediate gains and future implications. The folk theorem states that in infinite horizon games (those without a defined endpoint), many types of behavior can be supported by equilibrium as long as players believe future interaction is likely. This occurs because the threat of future consequences can influence current behavior.

Example

Suppose two ice cream shops compete in a small town:

Each shop can charge High ($5) or Low ($3) prices
If both charge High: Each earns $100/day
If both charge Low: Each earns $60/day
If one charges Low while other charges High: Low pricer gets $150; High pricer gets $30

Here’s the game in matrix format:

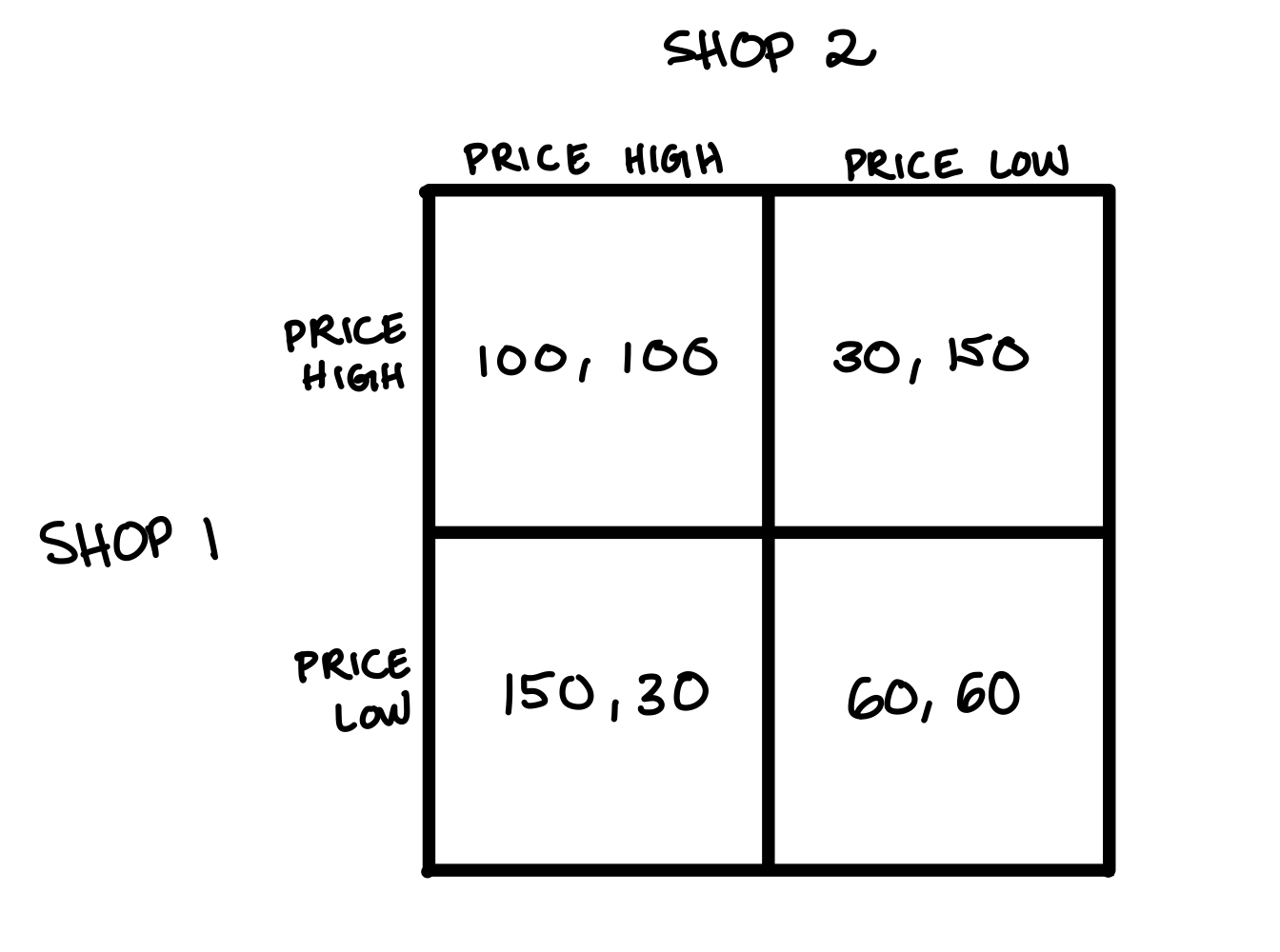
In a one-shot game, notice each player has a dominant strategy to price low. The equilibrium is where both players price low. But this is a prisoner’s dilemma, because if they cooperated and both priced high, they could capture higher payoffs.

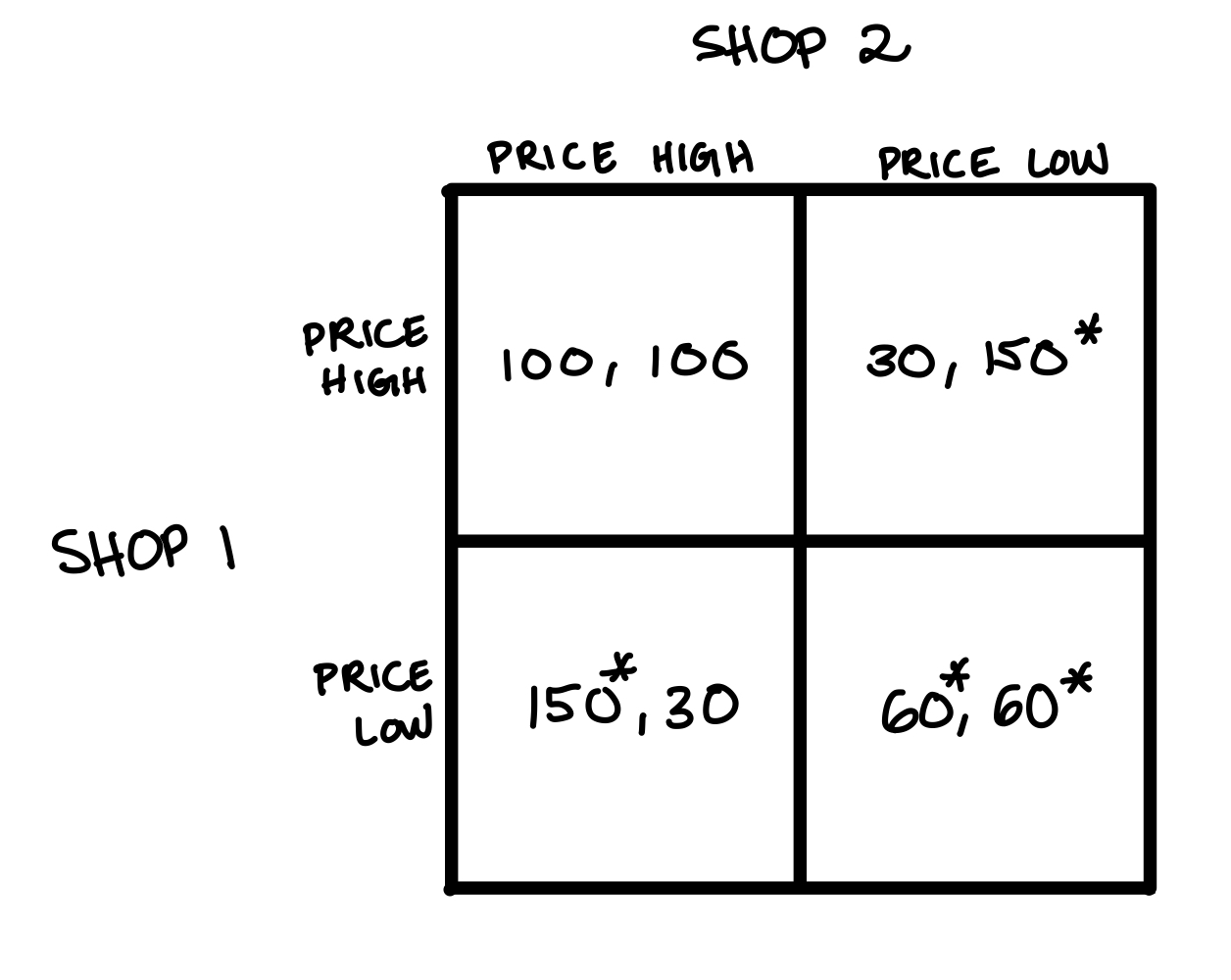
Now consider the two ice cream shops play this game on repeat. Each day, they set prices and receive payoffs, discounting at a rate of $\delta = 0.9$. Suppose shop 1 proposes an agreement: they agree to price High, but if shop 2 ever prices Low, shop 1 will retaliate by pricing Low forever after. This works to maintain a (High, High) outcome because the one-time gain from deviating to Low is $150 - $100 = $50, but then the firm has a future loss from a permanent price war, getting only $60 each period instead of the potential $100: $S = -40(.9) - 40 (.9^2) - 40 (.9^3) -...$, or $S = -360$. On net, the player can expect a $310 loss compared to staying true to their agreement.

Classwork 3) Repeated Games