24 Backward Induction

For more information on these topics, see Allen, Doherty, Weigelt, and Mansfield Chapter 12: Game Theory.

In this chapter, we’ll learn how to solve sequential games, which are strategic interactions where players make decisions in a specific order, with later players knowing the choices made by earlier players. We’ll visualize a sequential game using a game tree, like the ones we used in Chapter 18 when we studied risk.

A sequential game consists of subgames, which begin with a decision node and include all nodes that follow it in the game tree. Every game tree has at least one subgame, because the game as a whole is always one of its subgames.

The equilibria of a sequential game is a subgame perfect equilibrium (SPE): an equilibrium that remains optimal in every subgame of a sequential game, meaning players’ strategies constitute best responses not only for the entire game but also in every smaller game that could be reached during play.

The key principle for finding SPE’s is that when analyzing sequential decisions, you should work backwards using backward induction. The power of backward induction comes from systematically analyzing how current decisions interact with rational future responses. This provides a rigorous framework for strategic planning in sequential situations. An example will help to clarify:

24.1 Example 1: Market Entry Game

Consider a potential entrant deciding whether to enter a market, followed by an incumbent choosing to fight or accommodate:

The entrant moves first. They choose to enter or stay out.
If the entrant chooses to enter, the incumbant can either fight to maintain their market share, or accommodate.
Outcomes and payoffs for (entrant, incumbent):
- Stay out: (0, 100)
- Enter, fight: (-20, 40)
- Enter, accomodate (40, 60)

The game tree looks like this:

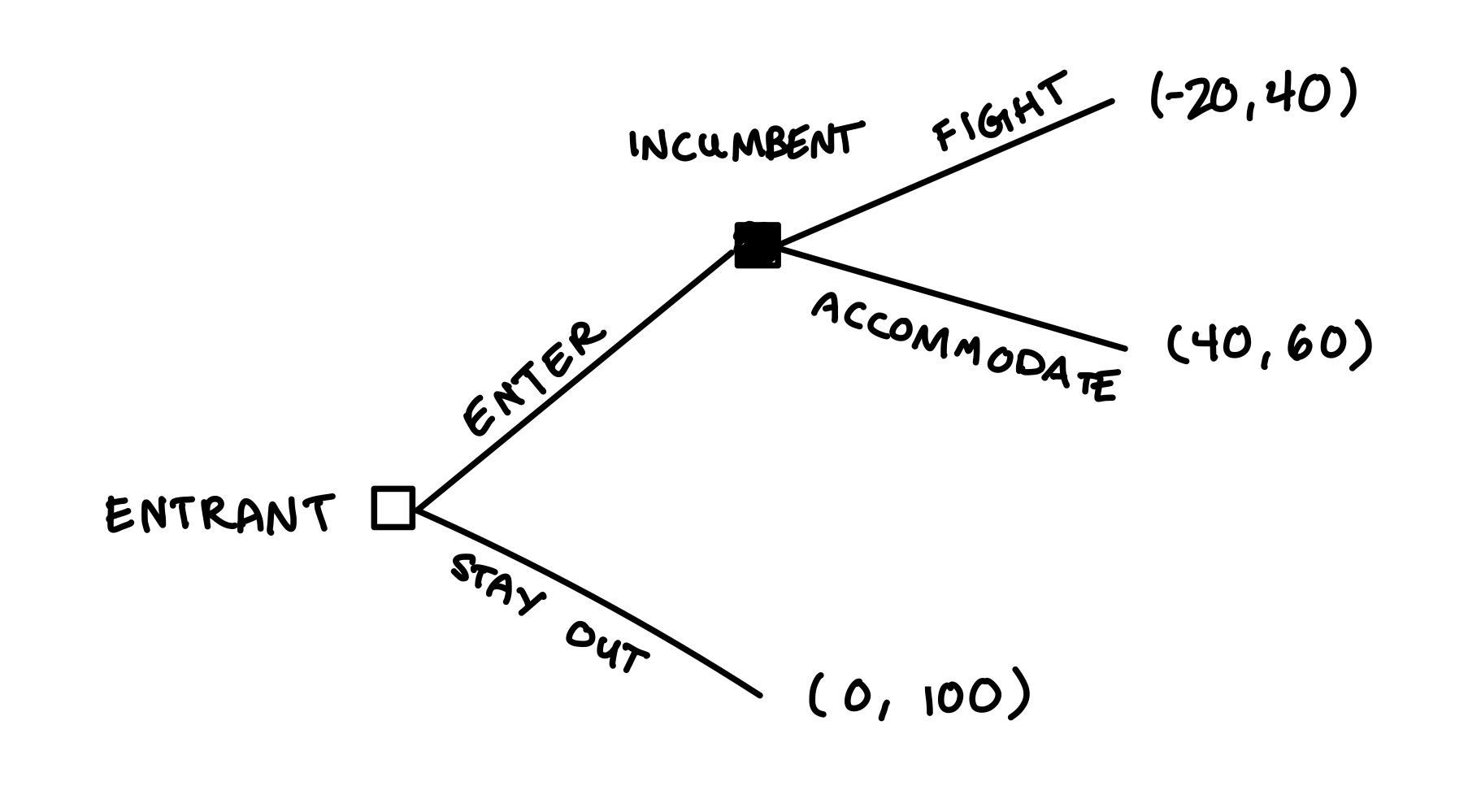
There are two subgames: the subgame that starts with the incumbent’s decision node and goes to the end, and also the entire game. The backward induction solution starts with the furthest along subgame and walks back:

Start with the last decision node: the incumbent’s choice of whether to fight or accommodate, assuming the entrant chooses to enter.
- If the incumbent chooses to fight, they will get a payoff of 40.
- If the incumbent chooses to accomodate, they will get a payoff of 60.
- Therefore, the incumbent will choose to accomodate when the entrant enters. Draw two lines through the branch where the incumbent fights because that branch will never be taken by the rational incumbent.

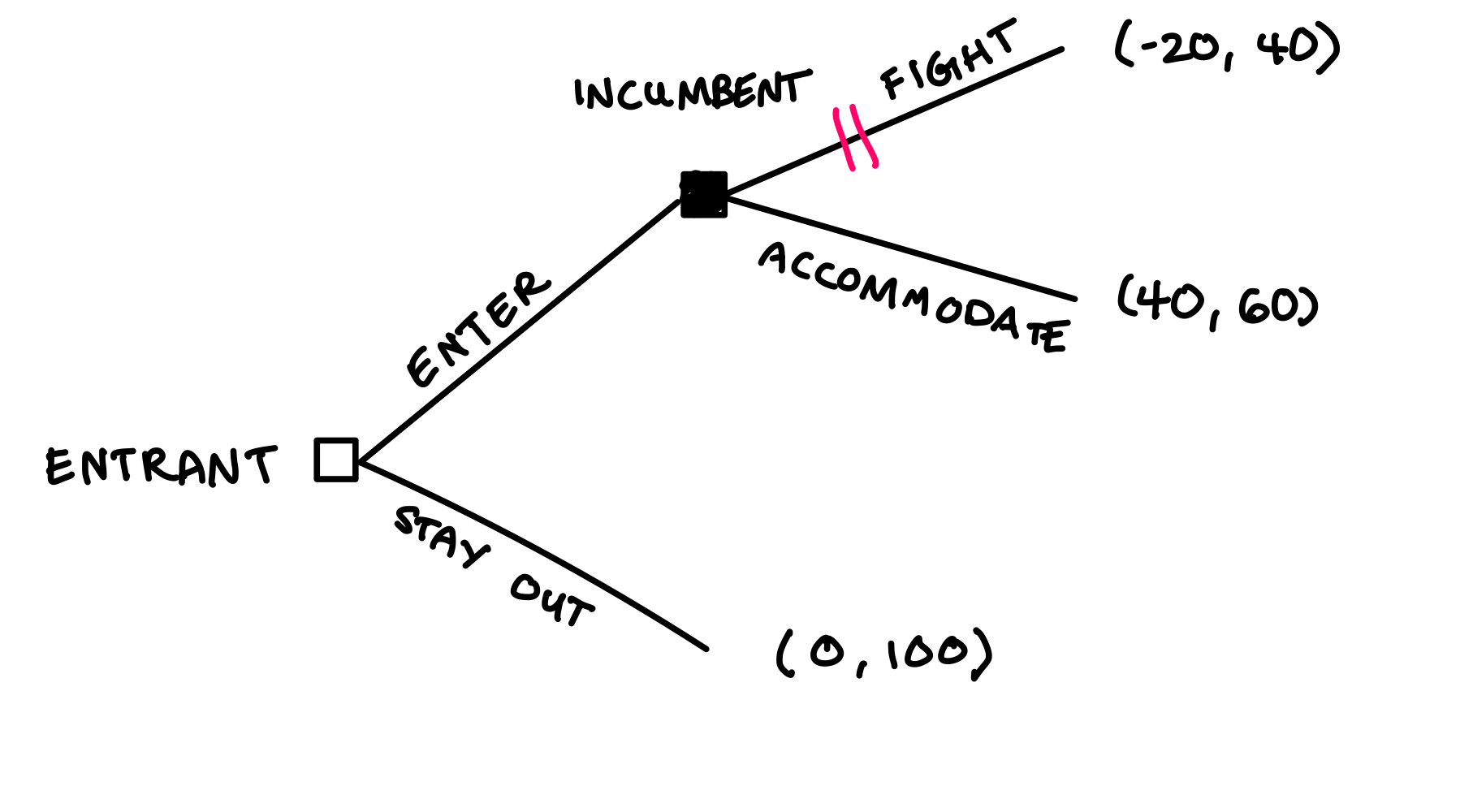
Back up to the entrant’s decision node. The entrant, anticipating that the incumbent will make the rational choice and accommodate if the entrant enters, faces this choice:
- Enter and get a payoff of 40
- Stay out and get a payoff of 0
- The entrant will choose to enter. Draw two vertical lines through the branch where the entrant stays out because that branch will never be taken by the rational entrant.

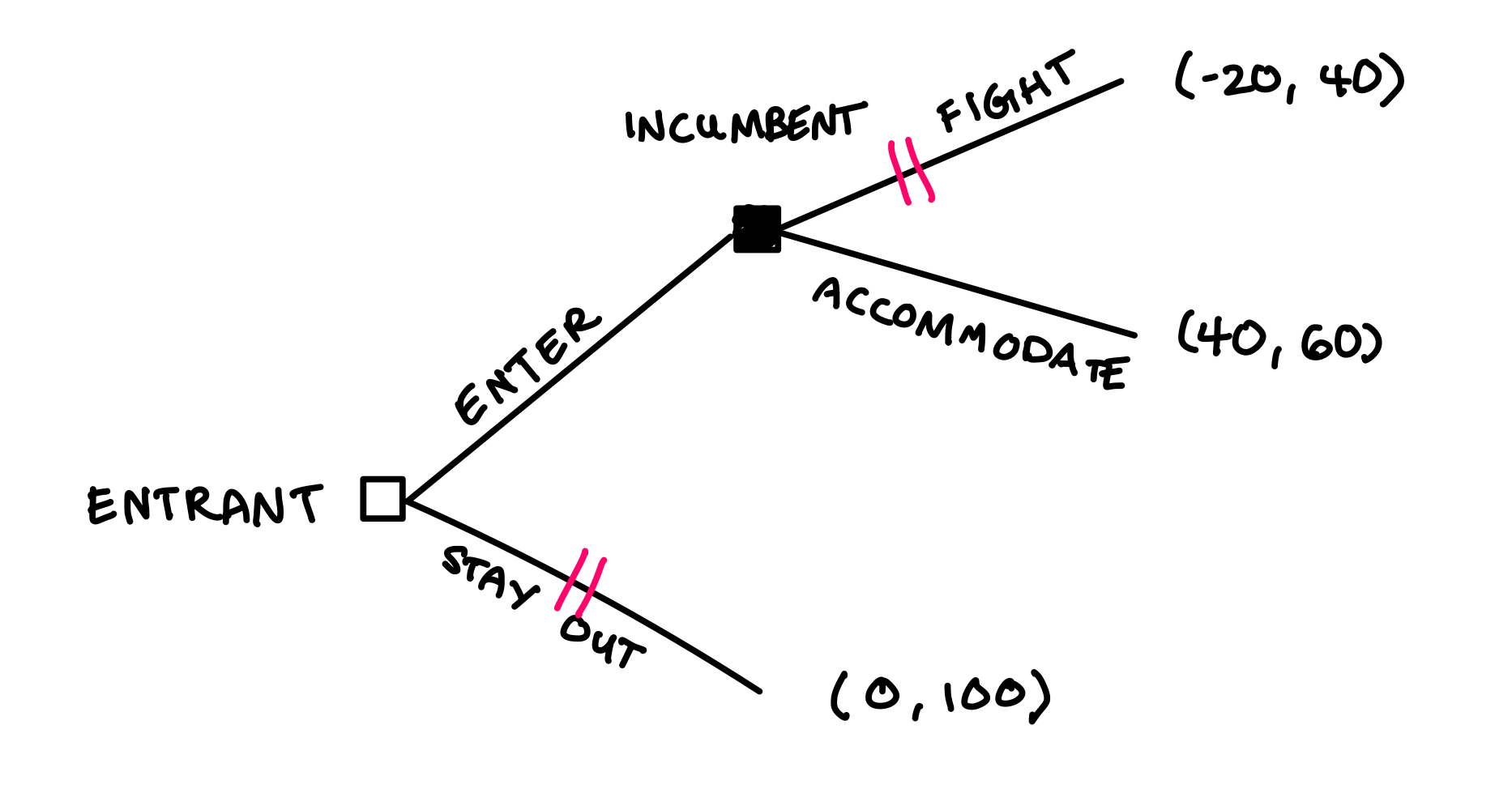
We’ve solved the game for the subgame perfect equilibrium: the entrant enters and the incumbent accommodates. Just like in the case of simultaneous games, the equilibrium is stable because no player can unilaterally switch strategies and realize a payoff gain.

24.2 Classwork 24

1) Market Entrant

Consider the same game as in example 1 in the workbook, but with new payoffs:
- Outcomes and payoffs for (entrant, incumbent):
  - Stay out: (0, 100)
  - Enter, fight: (-20, 50)
  - Enter, accomodate (30, 30)
Draw the game tree and solve for the SPE using backward induction. Draw two lines through branches you eliminate.
Consider again the same game as in example 1, but with new payoffs:
- Outcomes and payoffs for (entrant, incumbent):
  - Stay out: (0, 100)
  - Enter, fight: (X, Y)
  - Enter, accomodate (30, 30)
What conditions on X and Y must exist for the SPE to be (Enter, Fight)?

2) The Centipede Game

Two players alternate choosing to “Take” or “Pass”

If Take: Game ends
If Pass: Pot grows bigger

Payoffs grow as follows:
- Stage 1: (2,0) if Take, continue if Pass
- Stage 2: (0,4) if Take, continue if Pass
- Stage 3: (6,2) if Take, continue if Pass
- Stage 4: (4,8) if Take, end
Draw the game tree and solve for the SPE.
Suppose instead the payoffs for taking at stage 3 are (X, Y). Are there conditions on X and Y so that the players collaborate and grow the pot until stage 4? What are the conditions?

3) Product Quality Decisions

Consider sequential quality choices by two firms:

Firm 1 chooses High/Low quality first
Firm 2 observes and chooses High/Low second
Payoffs (Firm 1, Firm 2):
- High, High: (50, 40)
- High, Low: (30, 60)
- Low, High: (40, 30)
- Low, Low: (20, 20)
Draw the game tree and solve for the SPE.

Extra Credit: (+2 points)

Backward induction isn’t just for game theory—it’s a powerful tool for solving any problem with multiple sequential steps. Let’s look at a practical example:

Imagine a city map (shown in Figure 11.1) where:

Nodes represent intersections where drivers experience delays
Lines represent streets connecting these intersections
Numbers at each intersection show the delay time in minutes
The map connects residential areas to downtown parking lots

Our goal is simple: find the route from home to downtown that minimizes the total time spent waiting at intersections. You might think to solve this by checking every possible path—all 150 of them—and picking the fastest one. However, this brute-force approach is very inefficient.

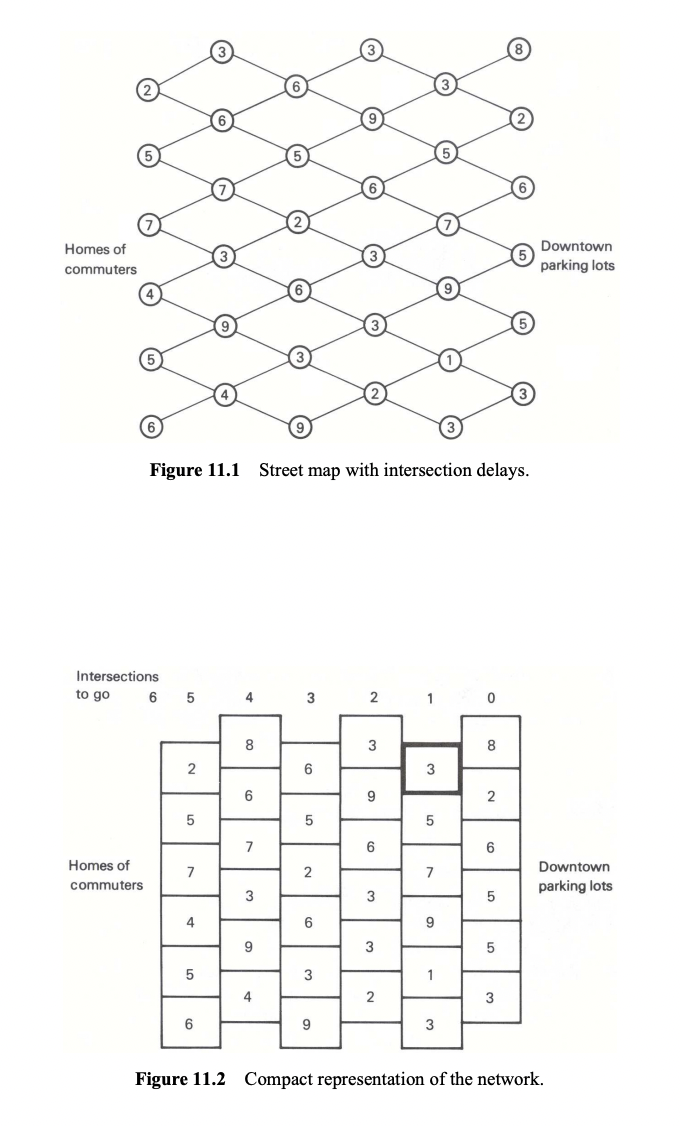
Let’s instead use backward induction, by working from downtown (right side) to home (left side):

Start with the final intersections (rightmost boxes):
- Here, there are no choices to make—you simply face whatever delay is shown
Next, look at intersections one step from the end:
- Take the highlighted box in Figure 11.2 as an example
- At this intersection, you face:
  - 3 minutes of delay at your current position
  - Plus a choice: move up (8 minutes delay) or down (2 minutes delay)
  - Best choice: Go down, for a total delay of 3 + 2 = 5 minutes
Repeat this process for every intersection in that column:
- Calculate the total delay (current delay + best next move)
- Mark the best choice with an arrow (up or down)
- Write the minimum total delay in bold (as shown in Figure 11.3)

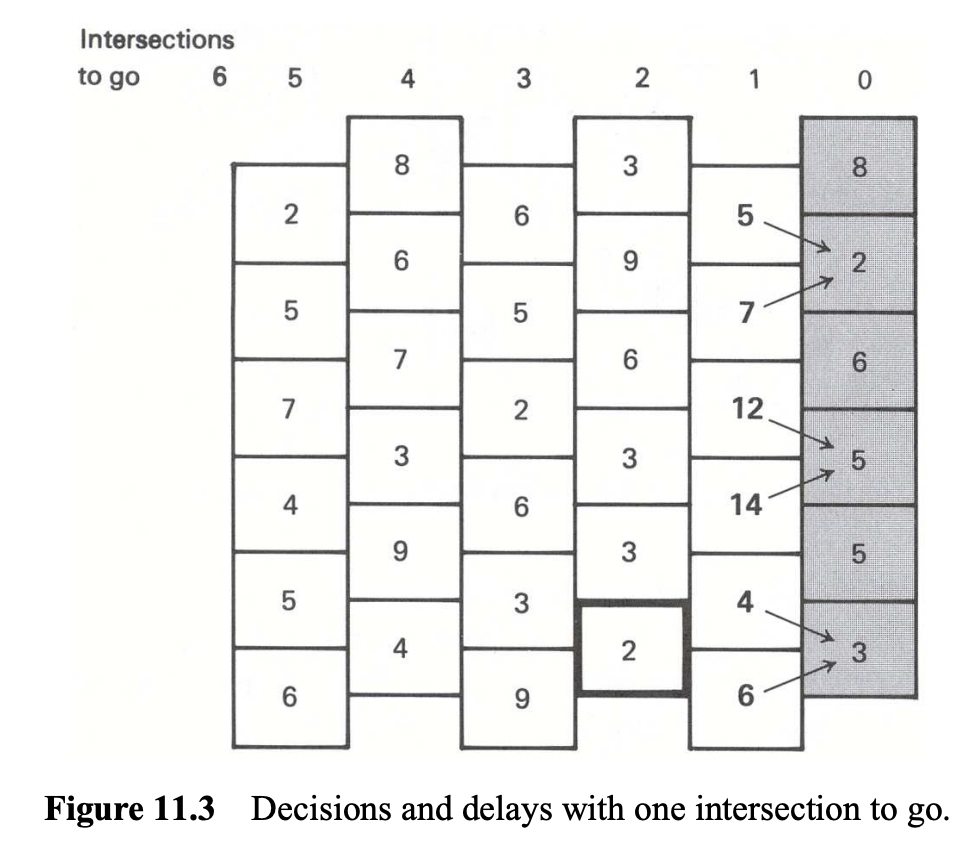
Use backward induction to solve the rest of the puzzle. Draw the optimal paths and report the lowest amount of time it takes to get to downtown from each of the six residential areas.