23 Dominant Strategies – Economics of Organizations

23.1 Game Theory Basics

Game theory provides leaders of organizations with tools to handle strategic decisions - those involving interactive payoffs where the consequences depend on both their actions and the actions of others. Unlike non-strategic decisions (like optimizing a shipping route), strategic decisions require considering how others will react and respond. This creates complexity since others are also thinking about your potential moves.

Every game theory model is defined by five key parameters:

The Players: These are the entities (individuals or groups) making decisions. Player identities matter since behavior often changes based on who you’re interacting with.
The Feasible Strategy Set: This includes all possible actions that players might realistically take. Failing to consider potential strategies can leave managers vulnerable to surprise moves.
The Outcomes/Consequences: These represent the intersection of player strategies - all possible end states based on the combinations of choices made.
The Payoffs: Each outcome has associated payoffs for each player based on their preferences. Players are assumed to be rational and prefer higher payoffs.
The Order of Play: Specifies whether moves are simultaneous or sequential. In simultaneous games, players act without knowing others’ choices.

23.2 Visual Representation

Games can be shown in two main formats: matrix form (best for simultaneous games) and a game tree (best for sequential games). In this classwork we’ll talk about matrix form; next classwork we’ll revisit game trees.

Matrix Form:

Shows all possible outcomes in a grid
Lists payoffs for each combination of strategies
Example: Two firms deciding whether to maintain or increase spending

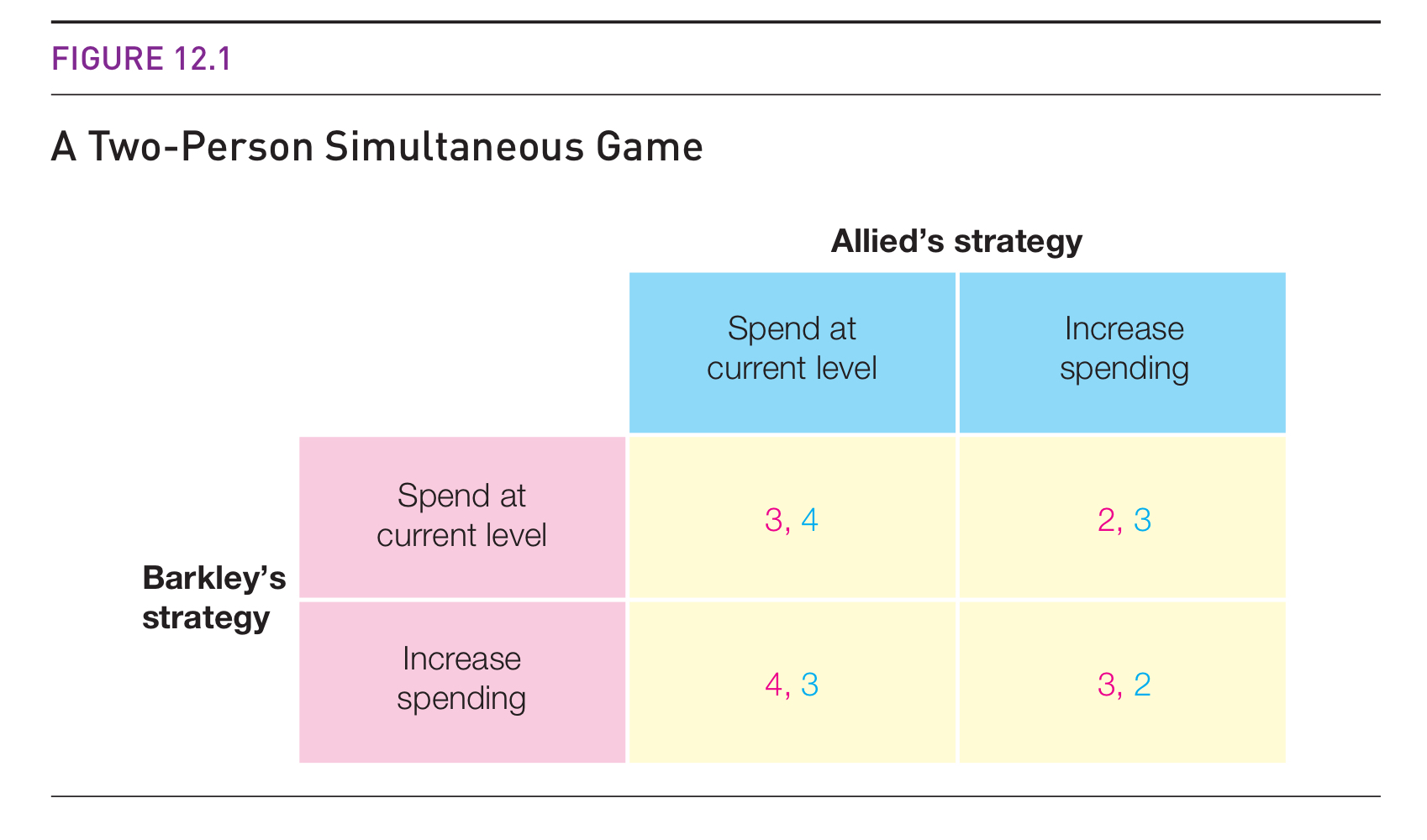
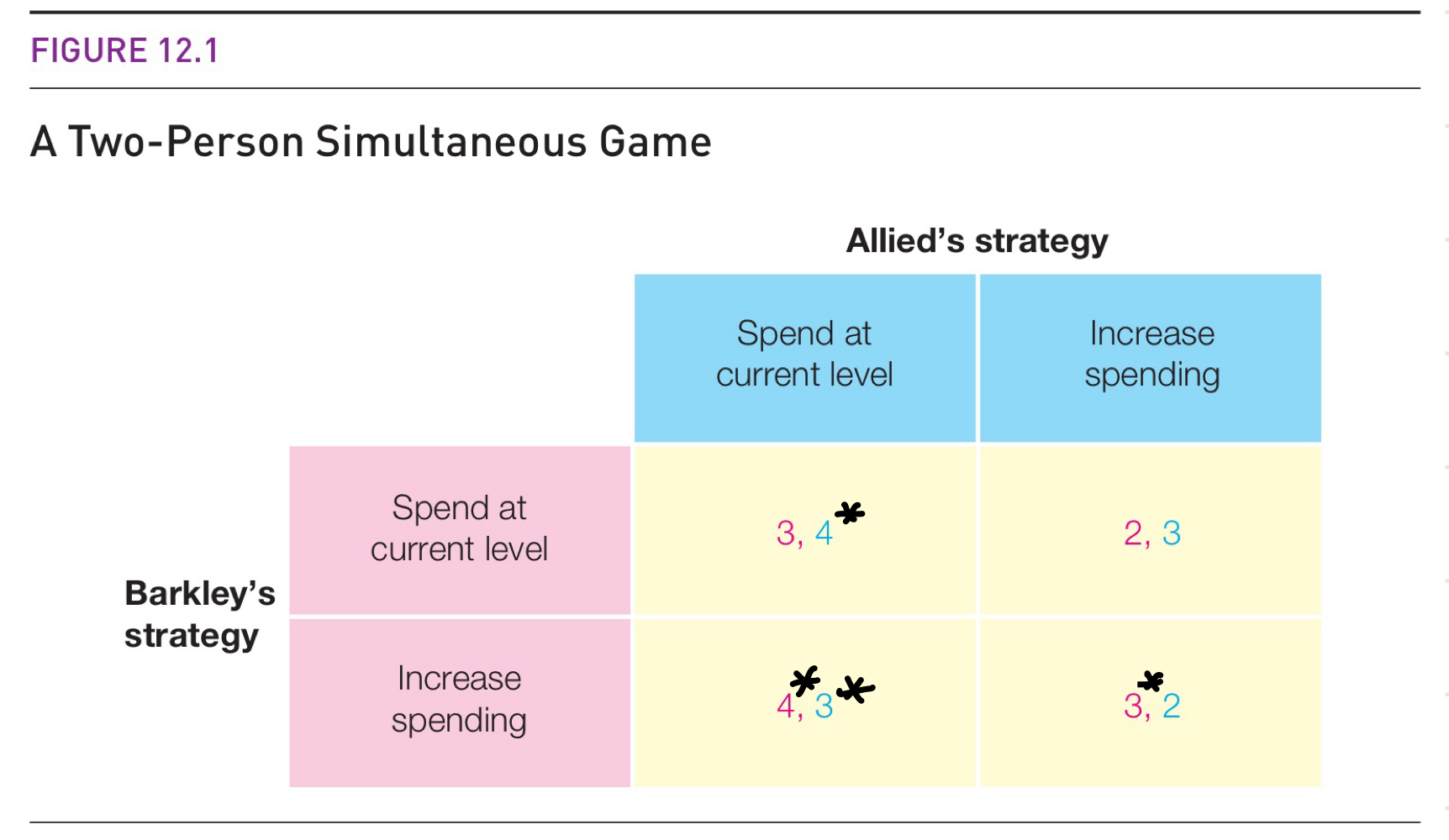
Here’s how to interpret the matrix above:

Players: Allied and Barkley
Feasible Strategy Set: Allied can spend at the current level or increase spending; Barkley has the same choices as Allied
Outcomes: Allied and Barkley might both spend at the current level, they might both increase spending, or one might increase spending while the other spends at the current level.
Payoffs: If both players spend at the current level, Allied gets a payoff of 4 and Barkley gets a payoff of 3. If both players increase spending, Allied gets a payoff of 2 and Barkley gets a payoff of 3. If Allied increases spending and Barkley does not, Allied gets 3 and Barkley gets 2. If Barkley increases spending and Allied does not, Allied gets 3 and Barkley gets 4.
Order of play: simultaneous.

Question 1: The Prisoner’s Dilemma and Cartels

The prisoner’s dilemma is a famous game theory scenario that illustrates why rational individual choices can lead to suboptimal collective outcomes. A classic business example is cartel agreements:

Consider two firms in a cartel agreeing to keep prices high:

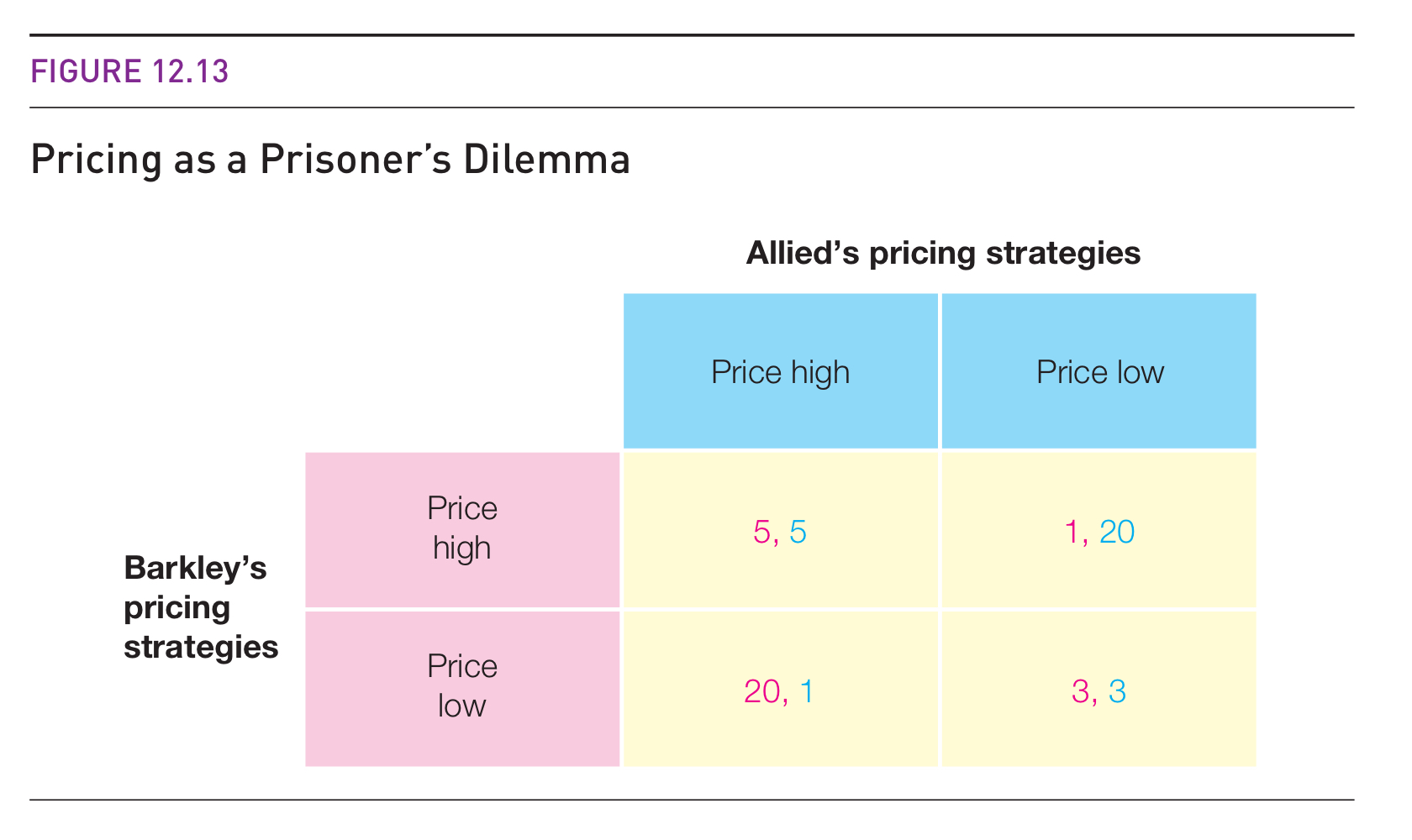
Who are the players?
What is the feasible strategy set?
What are the outcomes/consequences?
What are the payoffs?

23.3 Solution Concepts

Dominant Strategies

A dominant strategy is one that gives a higher payoff regardless of what others do. These are valuable since they:

Simplify decision making (no need to guess others’ moves)
Should always be chosen by rational players
Help eliminate obviously inferior options

For example, consider figure 12.1 again. Does Allied have a dominant strategy? To find out, consider what Allied should do (Allied’s best response) if Barkley spends at the current level. If Allied responds by spending at the current level, they earn a payoff of 4. If instead Allied responds by increasing spending, they earn a payoff of 3. So if Barkley spends at the current level, Allied’s best response is to spend at the current level. I put a star next to the payoff for Allied’s best response.

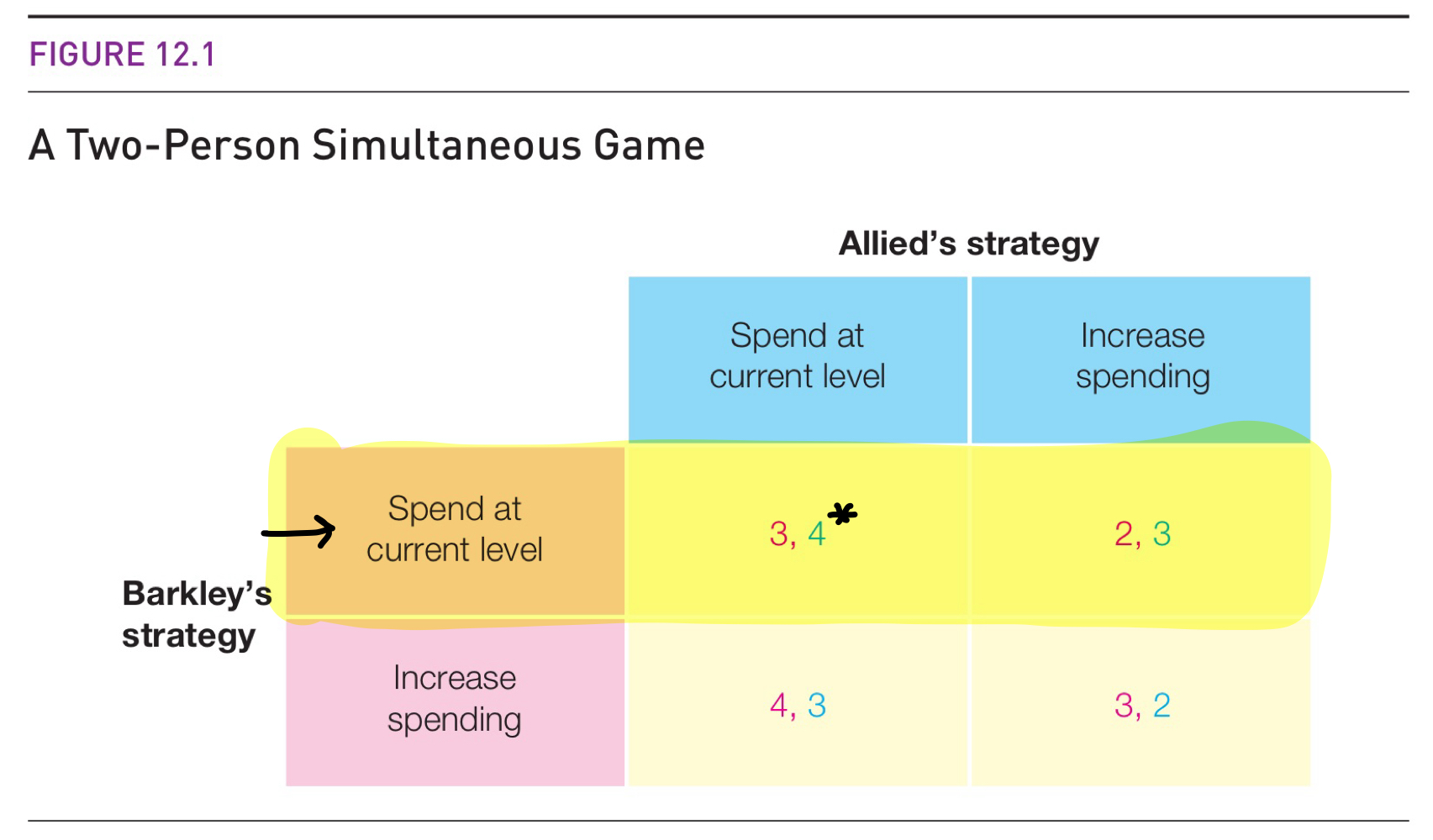
Now consider what Allied should do if Barkley increases spending. If Allied spends at the current level, they earn a payoff of 3. If Allied also increases spending, they earn a payoff of 2. So if Barkley increases spending, Allied should spend at the current level.

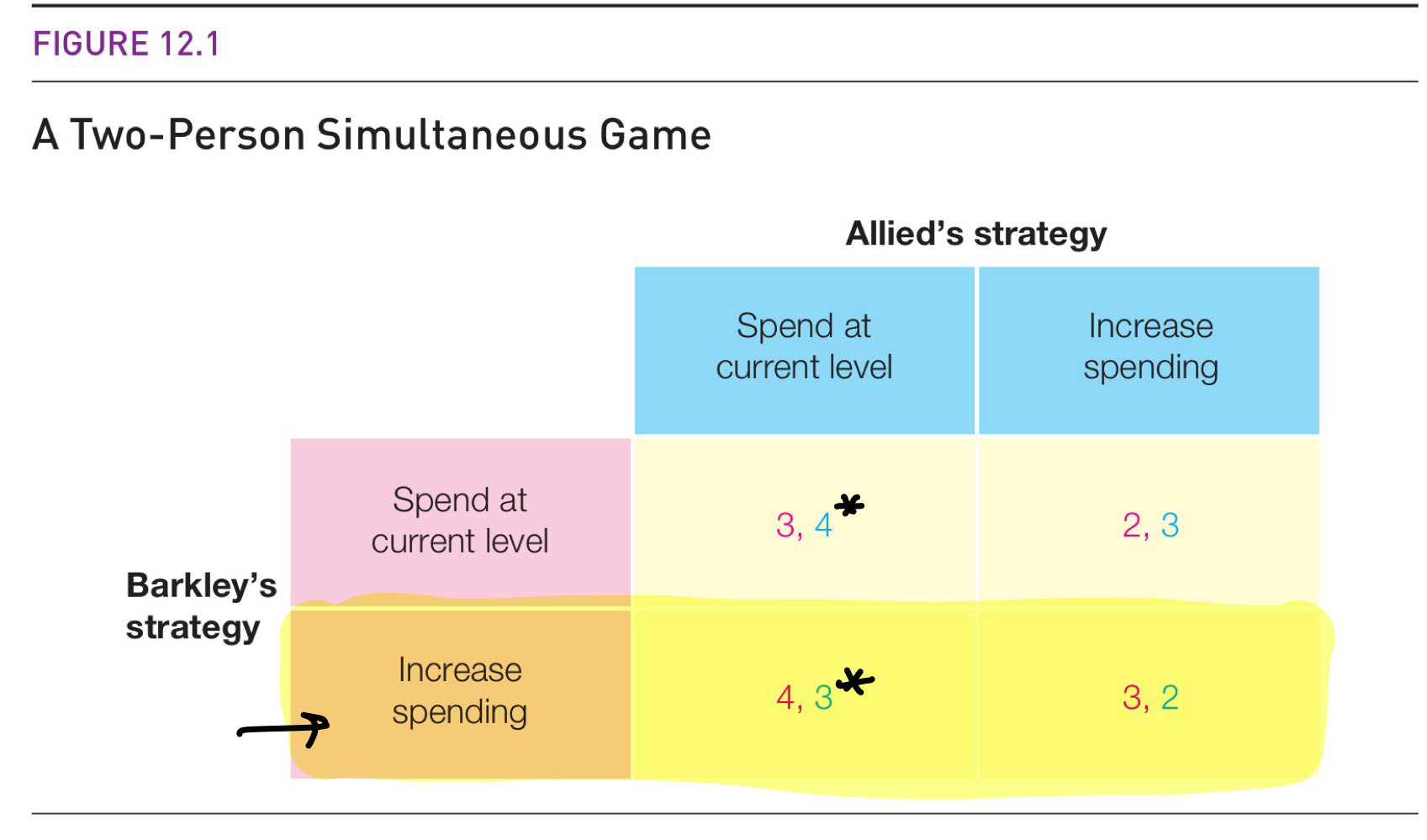
This is interesting: no matter what Barkley chooses to do, Allied is better off spending at the current level! That’s the definition of a dominant strategy. Allied has a dominant strategy and it is to spend at the current level.

Question 2: Dominant Strategies

Consider figure 12.1. Does Barkley have a dominant strategy, and if so, what is it?
Now consider figure 12.13. Find Allied’s dominant strategy and find Barkley’s dominant strategy (they will be the same because the game is symmetric). Which outcome has both players playing their dominant strategies?

Equilibrium

An equilibrium occurs when no player has incentive to unilaterally change their strategy. This provides stability since everyone is choosing their best response given what others are doing. The concept helps predict behavior since rational players should settle on equilibrium strategies.

If you put stars next to payoffs for best response strategies, it’s easy to find equilibria: if both payoffs have stars next to them, that means all players are playing their best responses. Because the strategy is their best response, that means they can’t unilaterally change their strategy and get a higher payoff. Verify this for yourself: the equilibrium in figure 12.1 (below) is where Allied spends at the current level and Barkley increases spending. This is stable because if Allied unilaterally switches strategies, they go from earning 3 to earning 2: it’s a loss. And if Barkley unilaterally switches strategies, they go from earning 4 to earning 3: it’s also a loss.

Question 3: Equilibrium

Consider the Prisoner’s Dilemma in figure 12.13.

Find the equilibrium (both payoffs have stars next to them, meaning both players are giving best responses).
Verify that the equilibrium is stable: if Allied unilaterally changes their strategy, they earn \(\underline{\hspace{8mm}}\) instead of \(\underline{\hspace{8mm}}\), which is a loss. And if Barkley unilaterally changes their strategy, they earn \(\underline{\hspace{8mm}}\). instead of \(\underline{\hspace{8mm}}\), which is also a loss.

Of course, this explains why cartels tend to break down - even though all members would benefit from cooperation, each has individual incentive to cheat.

Question 4: More Practice with Best Responses, Dominant Strategies, and Equilibrium

Suppose company X and company Y are deciding whether to adopt a new industry standard. Adoption costs 5 million but provides benefits of 8 million if both adopt or 2 million if only one adopts.

Draw the payoff matrix.
Label best responses with stars.
Do the companies have dominant strategies? Explain the intuitive reason.
Are there any equilibria (both players give best responses)? If so, explain why the equilibria are stable by analyzing unilateral changes in strategy.