3.6 Consumer’s Surplus

For more information on these topics, see Varian Chapter 14: Consumers’ Surplus.

A consumer’s surplus occurs when someone pays less for a product than the amount they were willing to spend. This assignment will help you understand how this surplus measures the economic benefit that consumers gain from being able to buy goods and services in the marketplace.

Demand for a Discrete Good

If good 1 is a discrete good, then it is only available in integer amounts (you can buy 0, 1, 2, etc units). Let’s think about how to describe the demand for good 1.

• If $p_1$ is way too high, the consumer won’t want to buy a single unit.
• If $p_1$ drops low enough, the consumer might buy one unit.
• If $p_1$ drops lower still, the consumer might buy a second unit.
• And so on.

So the demand for a discrete good is given by a list of reservation prices. For instance, if reservation prices are $(7,4,2,1)$, that means that the consumer won’t buy any units of good 1 until the price falls to $7, at which point the consumer will buy 1 unit. If the price fell to $4, the consumer would be willing to buy a second unit. If the price fell to $2, the consumer would be willing to buy a third unit, and if the price fell to $1, the consumer would buy a fourth unit. Here’s the demand curve for good 1 in a figure (it’s a step function):

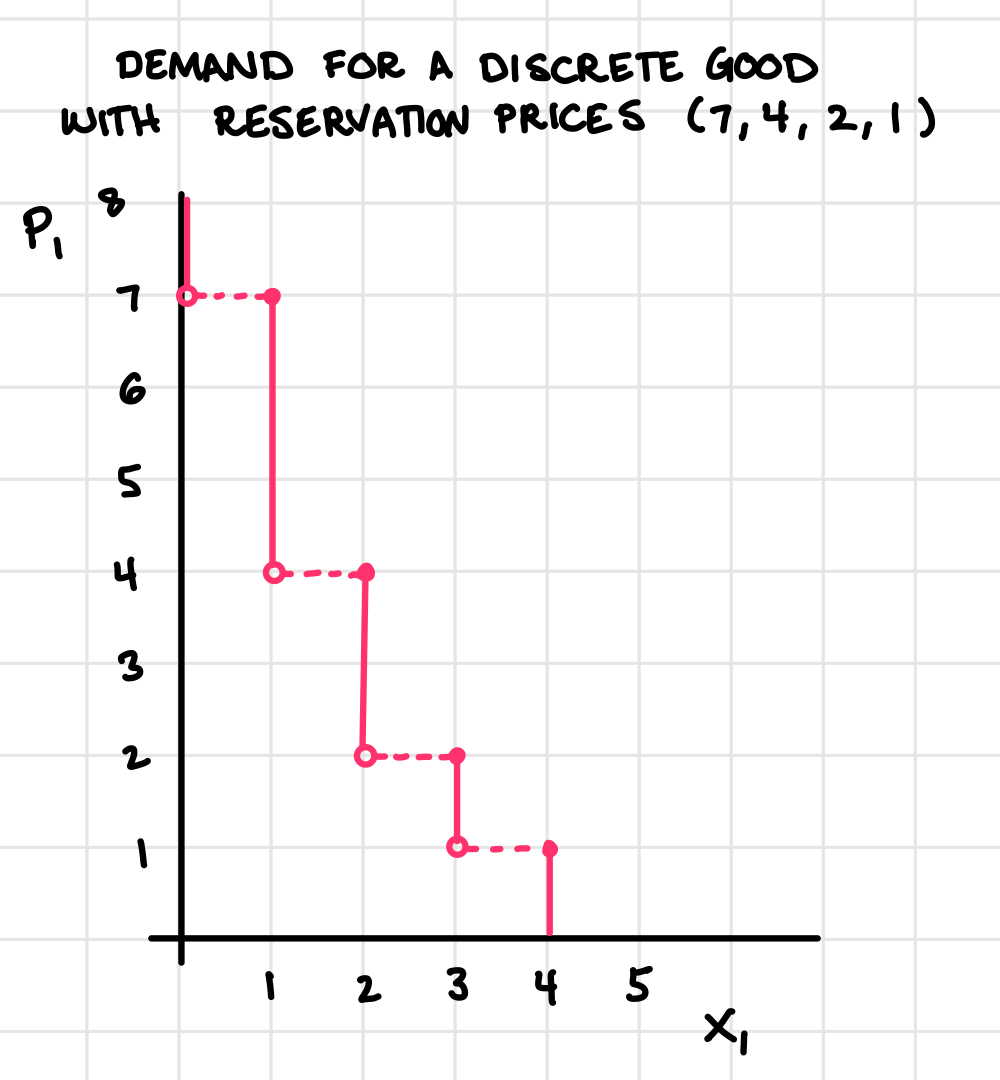
1) How many units of good 1 will the consumer with reservation prices (7, 4, 2, 1) choose when $p_1=3$? What about when $p_1=2$? And when $p_1=8$?

Answer:

Let’s think of a utility function that could describe this kind of demand.

• For simplicity, suppose that $u(0)=0$: consuming zero units of good 1 generates no utility for the consumer. Also assume the consumer gets 1 unit of utility for having one dollar.
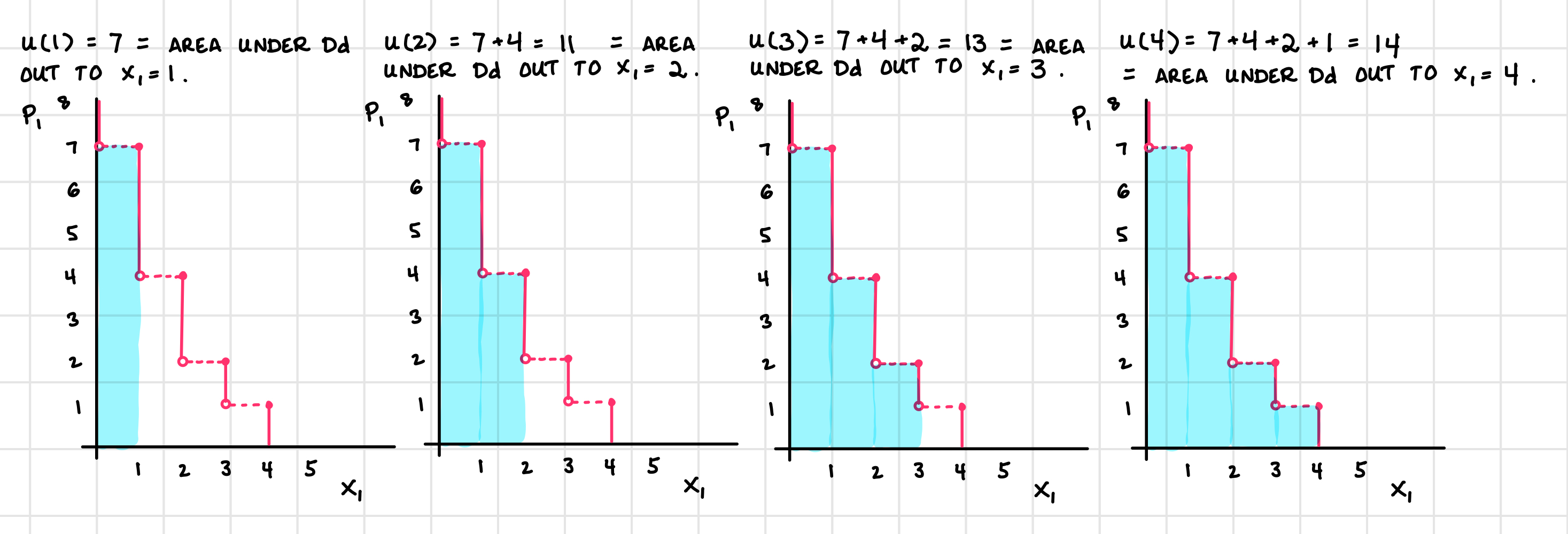
• How much utility would consuming one unit of good 1 yield? The consumer has a maximum willingness to pay of $7 for it, and at a price of $7, the consumer is just willing to buy it. So we could say it yields 7 units of utility for the consumer: $u(1)=r_1=7$.
• How much utility would consuming 2 units yield? The consumer would be willing to pay a maximum of $7 for the first unit, and then a maximum of $4 for the second unit, so the consumer is indifferent between having $7+4=11$ dollars and having two units of the good. Therefore, $u(2)=11$.

2) Following the pattern above, find the utility the consumer gets for having three, and then four units of the discrete good.

Answer:

Utility as the Area Under the Demand Function

Notice that this utility function is also the area under the demand curve: $u(1)$ is the area under the demand curve out to $x_1=1$, $u(2)$ is the area under the demand curve out to $x_1=2$, and so on.

If $p_1=5$, the consumer would purchase 1 unit, and they would get $u(1)=7$ from that unit. The total benefit to the consumer, or consumer surplus, from purchasing that unit is the utility of $7 minus the amount paid (one unit at a price of $5 means $5 was paid). So the consumer surplus would be $7-5=2$ dollars.

Consumer surplus is the difference between the total amount that consumers are willing to pay for a good and the total amount they actually pay. It represents the benefit or excess satisfaction that consumers receive when they purchase a product for less than the highest price they are willing to pay. Graphically, it is the area under the demand curve and above the price level, up to the quantity purchased.

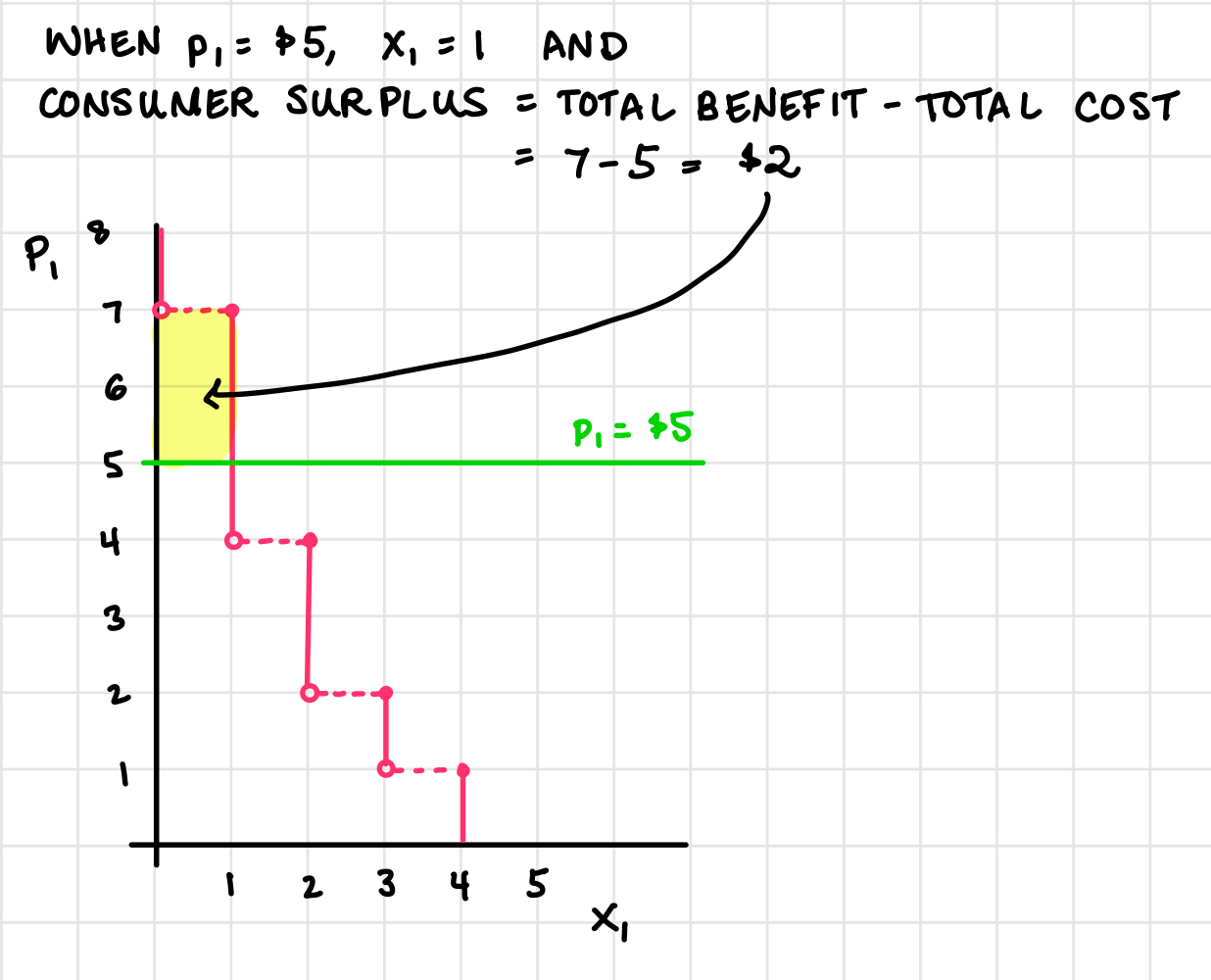
3) Using the demand function above, suppose that $p_1=2$. How many units of good 1 does the consumer buy? What is the consumer surplus?

Answer:

Approximating a Continuous Demand

If $x_1$ is not a discrete good, demand might be something like this continuous curve:

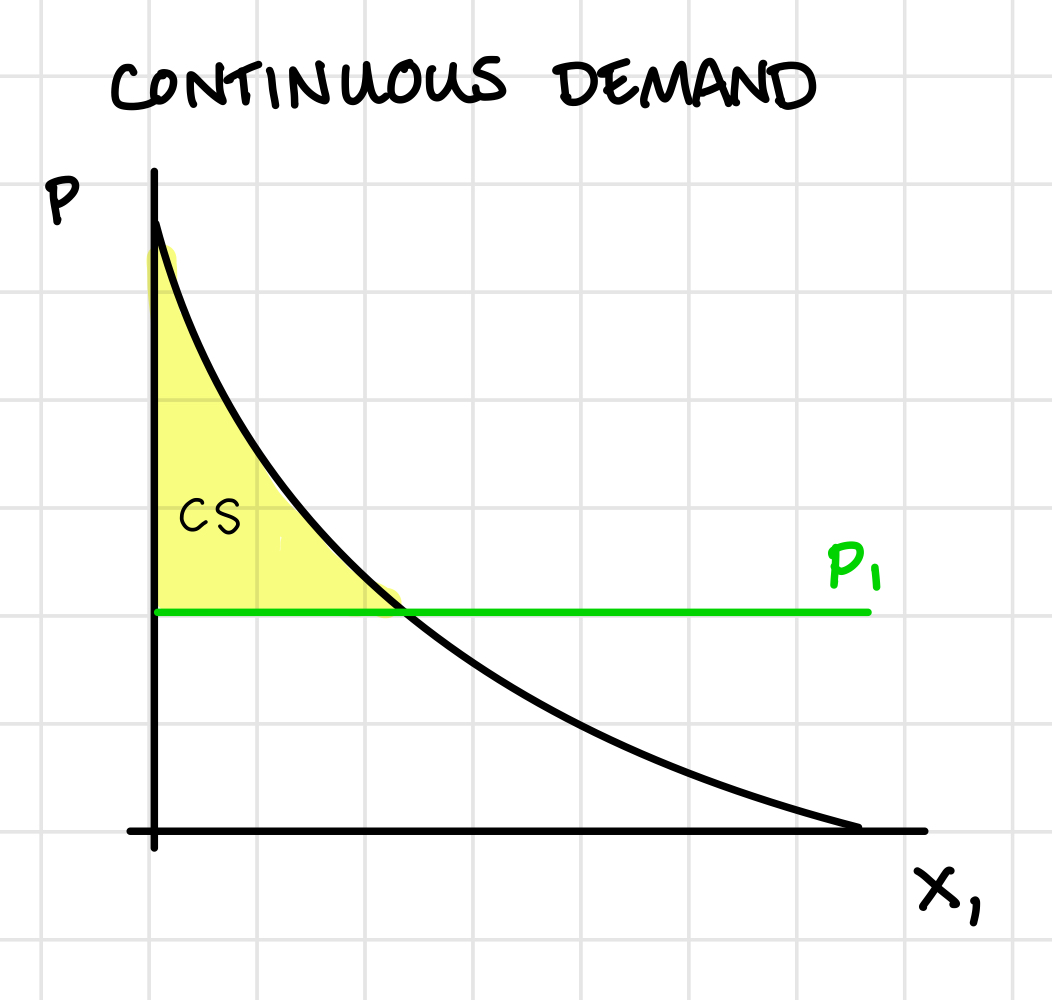
In which case, the consumer surplus is still just the area under the demand curve and above the price that the consumer pays.

Interpreting a Change in Consumer Surplus

4) Let the demand for a good be given by $x_1=10-p_1$. If $p_1$ falls from $3 to $2, what is the change to consumer surplus?

Answer: