3.4 Preferences and Utility

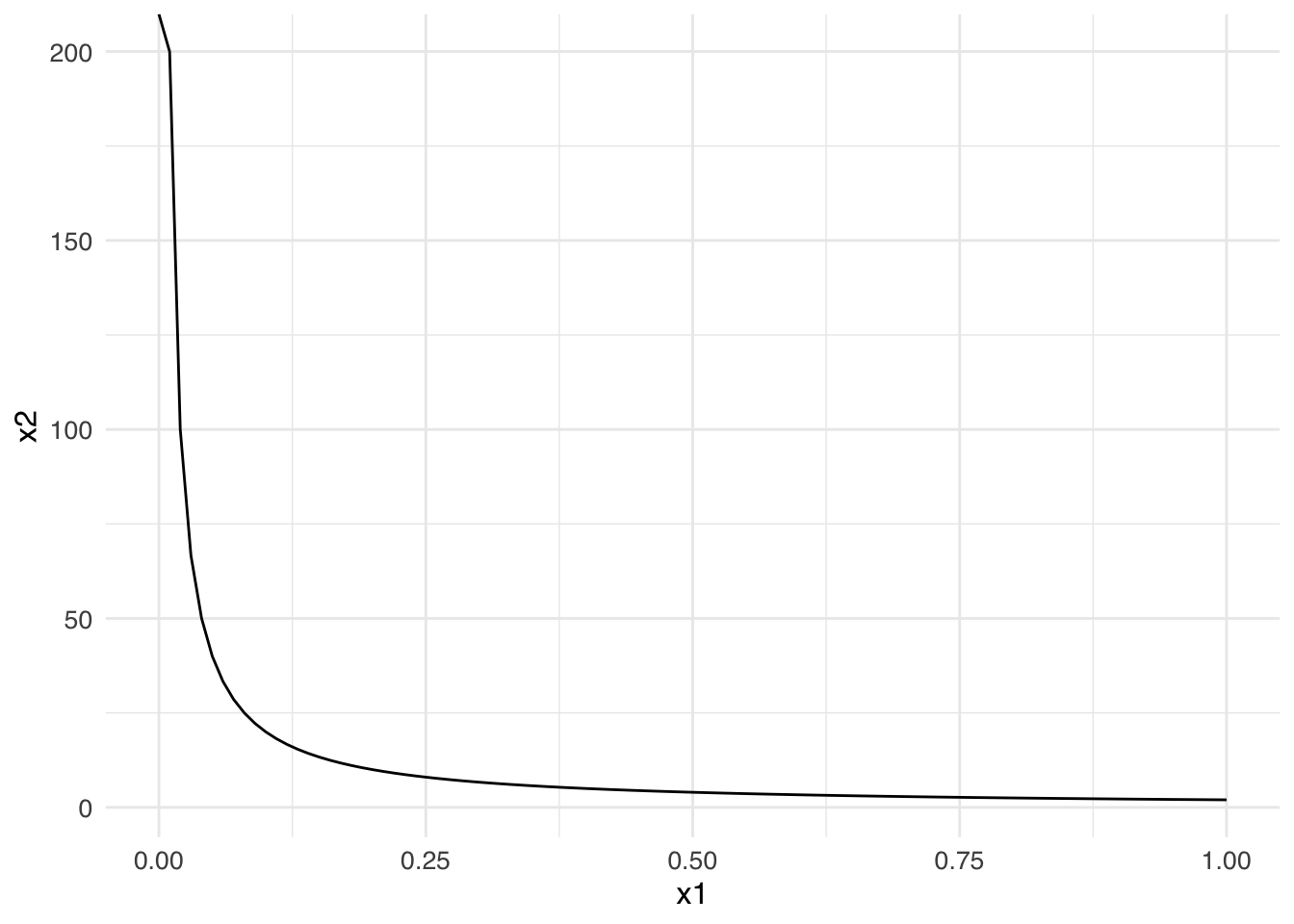
For more information on these topics, see Varian Intermediate Microeconomics Chapter 3: Preferences and Chapter 4: Utility.

In the last chapter, I explained how consumers choose the best bundle of goods they can afford, detailing what “afford” means in precise terms. In this chapter, I will provide a similarly detailed explanation of what might constitute the “best bundle.”

Preference Notation

The idea of preference is based on a consumer’s behavior. If a consumer never chooses Bundle 2 when Bundle 1 is available, that indicates a preference for Bundle 1.

For example, consider these two bundles:

Bundle 1: 3 graham crackers and 1 hot cocoa packet
Bundle 2: 1 graham cracker and 3 hot cocoa packets

If you choose Bundle 1 when both options are available, it means you prefer Bundle 1 to Bundle 2, or at least you are indifferent between them. In precise terms, Bundle 1 is at least as good as Bundle 2 to you.

Preference Notation: \(\succ\), \(\succeq\), \(\sim\)

\((x_1, x_2) \succ (y_1, y_2)\): This means that \((x_1, x_2)\) is strictly preferred over \((y_1, y_2)\). For example, if you would only choose Bundle 2 if Bundle 1 was not available, that indicates you strictly prefer Bundle 1.
\((x_1, x_2) \succeq (y_1, y_2)\): This means that \((x_1, x_2)\) is at least as good as \((y_1, y_2)\). If you choose Bundle 1, it indicates that Bundle 1 is at least as good as Bundle 2, even if you might be indifferent between them.
\((x_1, x_2) \sim (y_1, y_2)\): This means that the consumer is exactly indifferent between \((x_1, x_2)\) and \((y_1, y_2)\). If you have no preference between 3 graham crackers and 1 hot cocoa packet versus 1 graham cracker and 3 hot cocoa packets, then you are indifferent between the two bundles.

1) If \((x_1, x_2) \succeq (y_1, y_2)\) but it is not true that \((x_1, x_2) \sim (y_1, y_2)\), then:

\((x_1, x_2) \succ (y_1, y_2)\)
\((y_1, y_2) \succ (x_1, x_2)\)
\((y_1, y_2) \succeq (x_1, x_2)\)
None of the above

Answer:

Indifference Curves

An Indifference Curve through a consumption bundle \((x_1, x_2)\) consists of all other bundles \((y_1, y_2)\) such that \((x_1, x_2) \sim (y_1, y_2)\).

2) Consider these indifference curves. Which of the following is not supported by the diagram?

You prefer having 2 instant noodles and 4 jalapenos over having 2 instant noodles and 1 jalapeno
You are indifferent between having 4 instant noodles and 1 jalapeno and having 3 instant noodles and 4 jalapenos
If you had 2 instant noodles and 1 jalapeno, you’d be indifferent between getting an extra instant noodle and getting 3 more jalapenos
If you had 3 instant noodles and 1 jalapeno, you’d be indifferent between getting an extra instant noodle and getting 3 more jalapenos
None of the above

Answer:

Marginal Rate of Substitution

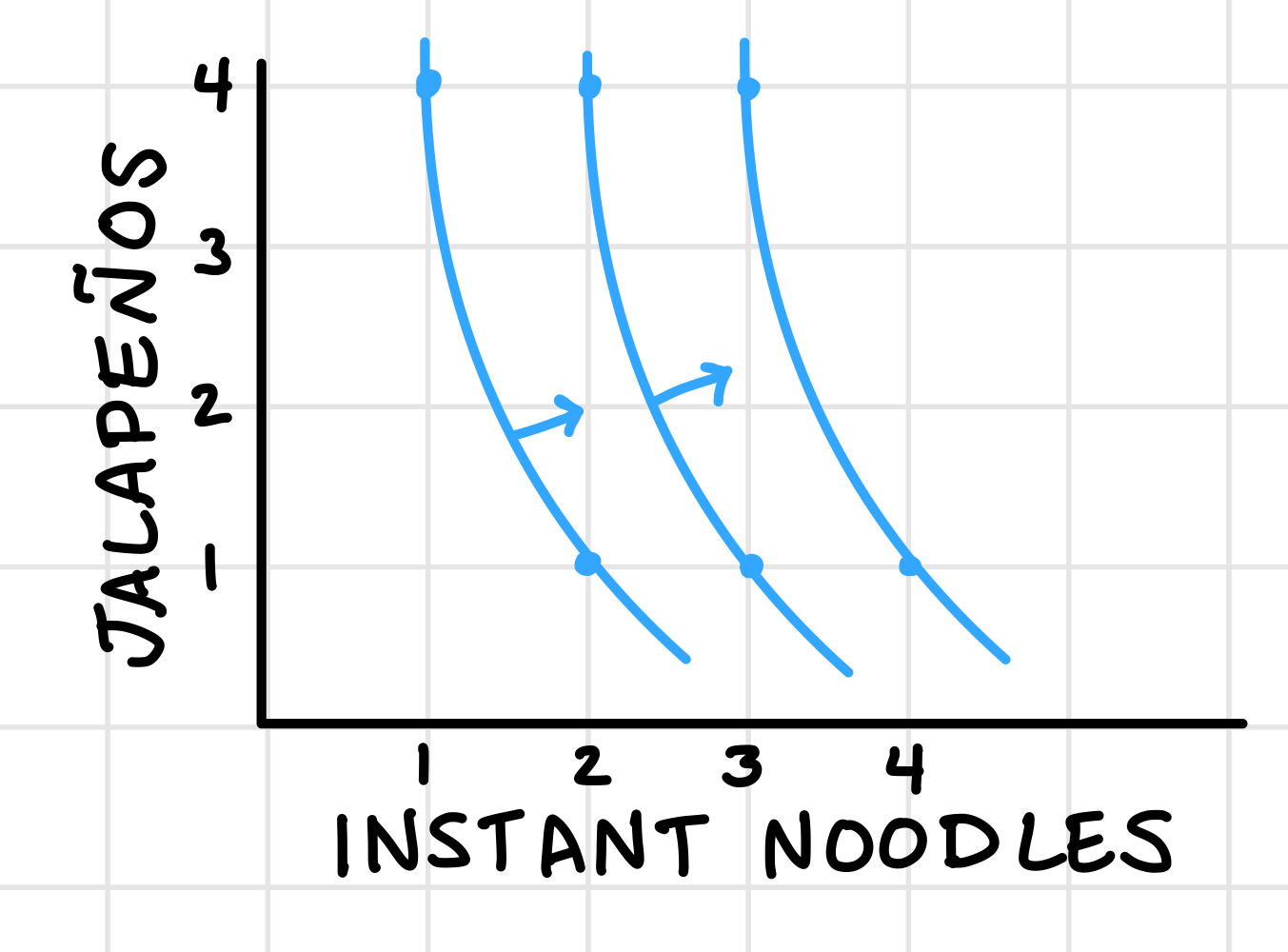
Question 2 eluded to the fact that the slope of the indifference curve represents a person’s marginal rate of subtitution (MRS): the rate at which you are just willing to substitute one good for the other.

If you have 2 instant noodles and 1 jalapeno, you’re indifferent between getting an extra instant noodle or getting 3 more jalapenos. In other words, your MRS is the negative of the slope of the indifference curve tangent line: \(\frac{\text{rise}}{\text{run}} = \frac{\Delta x_2}{\Delta x_1} = \frac{3}{1}\).

3) Suppose your marginal rate of substitution between kiwis (\(x_1\)) and limes (\(x_2\)) is 2. Then you’d be indifferent between getting 4 more kiwis and ___ more limes.

Answer:

4) Perfect substitutes are goods that can always be used interchangeably.

For instance, if I’m just as happy using butter or margarine to make cookies, then butter and margarine are perfect substitutes for me. Suppose I need a cup of butter or a cup of margarine to make a batch of cookies (and for example, .93 cups to make .93 batches of cookies). I can mix butter and margarine, so if I have half a cup of both, I can make 1 batch of cookies. Assume I’d always prefer to be able to make more cookies than less.

I’m indifferent between getting 0.5 cups of butter and ___ cups of margarine, so my marginal rate of substitution is ___.

Answer:

5) Perfect Complements are goods that are always consumed together in fixed proportions, like right shoes and left shoes.

Having an extra left shoe does me no good, but I’d rather have more pairs of shoes than less.

If you currently have 0 right and 0 left shoes, which of these bundles would you be indifferent to, and which bundles would you prefer?

1. Getting 1 right and 1 left shoe
1. Getting 1 right and 10 left shoes
1. Getting 10 right and 1 left shoes
1. Getting 2 right and 10 left shoes

Answer:

Utility Functions

Utility is a concept used to describe preferences. A utility function \(u(x_1, x_2)\) assigns a numerical value to every possible consumption bundle, ensuring that more-preferred bundles receive higher values than less-preferred bundles. Geometrically, a utility function is just a way to label indifference curves, with larger numbers corresponding to more preferred bundles.

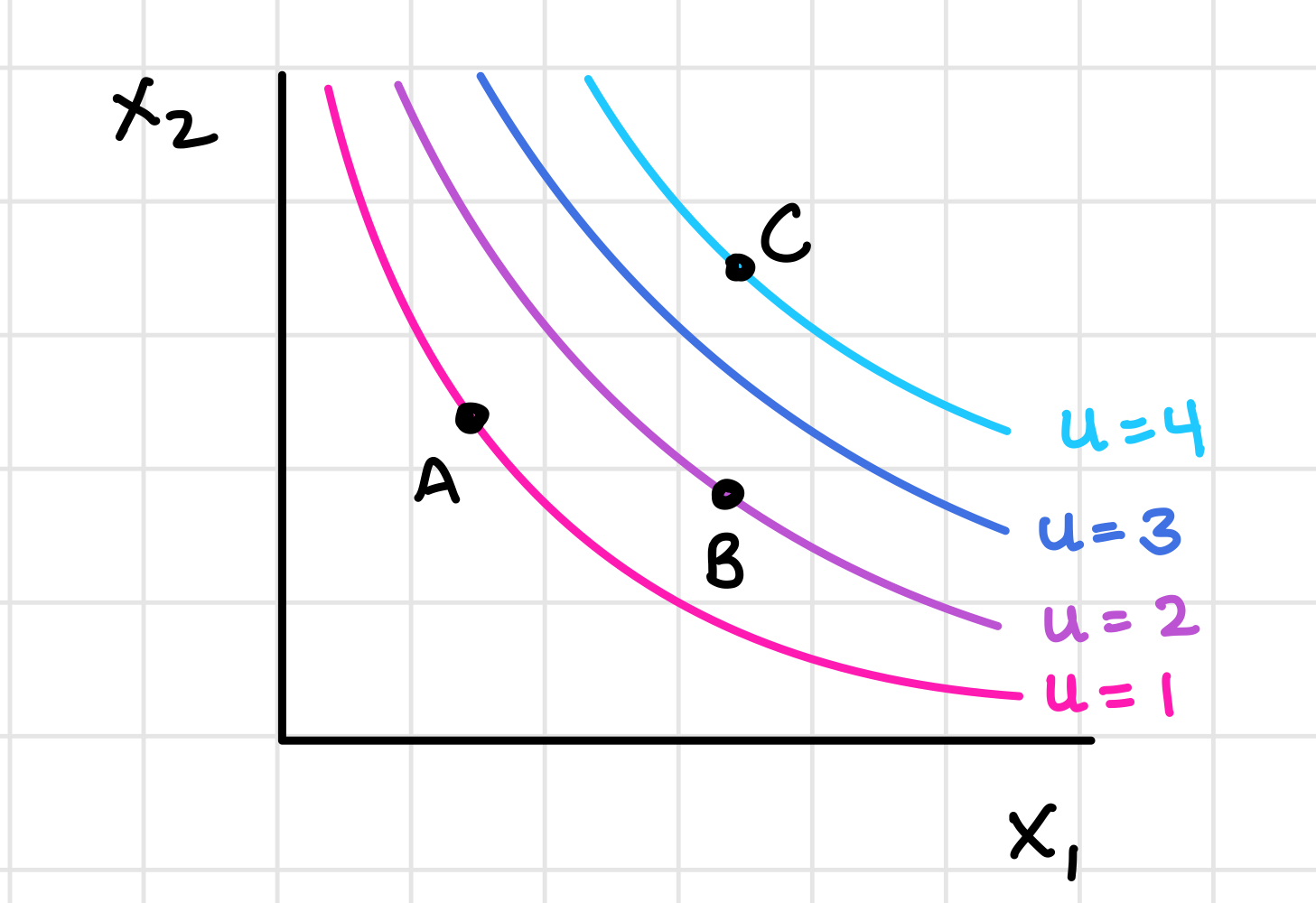
The crucial aspect of a utility function is its ability to rank bundles of goods in order of preference. The numerical difference between the utility values of two bundles is not significant. Therefore, if bundle \(A \succ B\) (A is preferred over B) and \(B \succ C\) (B is preferred over C), the following utility assignments for bundles \(A\), \(B\), and \(C\) are all valid:

Bundle	\(U_1\)	\(U_2\)	\(U_3\)
A	3	17	-1
B	2	10	-2
C	1	.002	-3

These assignments show that the preference ordering (A over B, B over C) remains consistent, even though the actual number value of utility offered by each bundle differs.

Monotonic Transformations

Since the ranking of bundles is what matters in a utility function, there are infinite ways to assign utilities to bundles of goods for a given set of preferences. As long as the utility function maintains the same order of ranking among the bundles, it is considered valid.

In other words, if \(u(x_1, x_2)\) is a utility function that represents a given set of preferences, then any monotonic transformation of \(u\) would also be a valid way to describe the same preferences. A monotonic transformation changes one set of numbers into another while preserving their order. For example, adding 2 to each value is a monotonic transformation, so \(U_2\) would represent the same preferences as \(U_1\):

Bundle	\(U_1\)	\(U_2 = U_1 + 2\)
A	3	5
B	2	4
C	1	3

6) Is multiplication by a positive number a monotonic transformation? That is, does \(U_2 = 2 U_1\) represent the same preferences as \(U_1\)?

Bundle	\(U_1\)	\(U_2 = 2 U_1\)
A	3	6
B	2	4
C	1	2

Answer:

Multiplying by a negative number reverses the ranking of bundles, so multiplying by a negative number would not be a monotonic transformation.

The way to determine if a function is a monotonic transformation is to take the derivative: if it’s always positive, you have a monotonic transformation.

Examples:

\(x + 2\) is a monotonic transformation because the derivative is 1, which is always positive:

\[\begin{align} f(x) &= x + 2\\ f'(x) &= 1 \end{align}\]

\(2x\) is a monotonic transformation because the derivative is 2, which is always positive: \[\begin{align} f(x) &= 2 x\\ f'(x) &= 2 \end{align}\]
Consider the natural log: \(f(x) = ln(x)\). It is only defined for \(x > 0\). The derivative is \(\frac{1}{x}\), which is always positive because \(x\) is always positive in the domain of \(f\). Therefore, the natural log is a monotonic transformation. \[\begin{align} f(x) &= \ln(x)\\ f'(x) &= \frac{1}{x} \end{align}\]

7) Consider the square root function: \(f(x) = \sqrt{x}\). Let \(x > 0\). \(f'(x)\) is ___, which is always positive because \(x\) is always positive. Therefore, the square root is a monotonic transformation.

\(\frac{1}{2x}\)
\(\frac{-1}{2x}\)
\(\frac{1}{2\sqrt{x}}\)
\(\frac{-1}{2\sqrt{x}}\)

Answer:

Drawing Indifference Curves using Utility Functions

You can use utility functions to draw indifference curves. For example, take the utility function \(u(x_1, x_2) = x_1 x_2\). Remember that an indifference curve is defined by all the bundles \((x_1, x_2)\) such that the consumer is indifferent to all of them. So to figure out all the bundles with a utility of 2, we can do this:

\[x_1 x_2 = 2\]

Solve for \(x_2\) because it’s on the y-axis to put the equation into “slope-intercept form”:

\[x_2 = \frac{2}{x_1}\] And then plot that level curve using R:

library(tidyverse)

ggplot() +
  stat_function(fun = function(x1) 2/x1) +
  labs(x = "x1", y = "x2")

Add the level curves for 1, 3, 4, and 5:

ggplot() +
  stat_function(fun = function(x1) 1/x1, color = "red") +
  stat_function(fun = function(x1) 2/x1, color = "orange") +
  stat_function(fun = function(x1) 3/x1, color = "yellow") +
  stat_function(fun = function(x1) 4/x1, color = "green") +
  stat_function(fun = function(x1) 5/x1, color = "blue") +
  labs(x = "x1", y = "x2")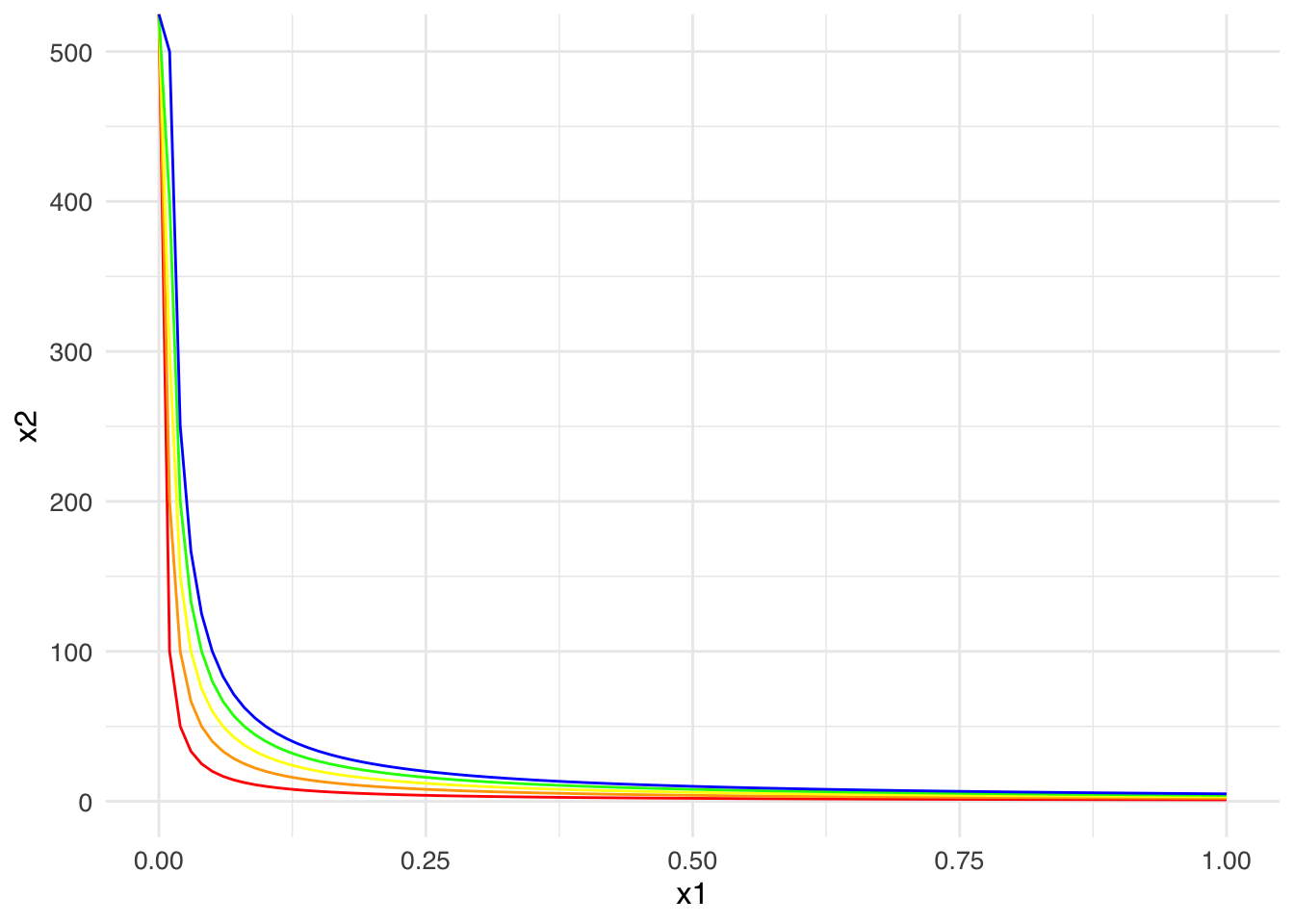

8) Take the utility function \(u(x_1, x_2) = x_1 + x_2\).

Use R to draw level curves for \(u = 1\), \(u = 2\), and \(u = 3\).

Answer:

We learned that the Marginal Rate of Substitution measures the absolute value of the slope of an indifference curve, and it can be interpreted as the rate at which a consumer is just willing to substitute a small amount of good 2 (\(dx_2\)) for good 1 (\(dx_1\)), such that utility doesn’t change (\(du = 0\)). Consider the total differential \(du = \frac{\partial u(x_1, x_2)}{\partial x_1} dx_1 + \frac{\partial u(x_1, x_2)}{\partial x_2} dx_2\): this approximates how much \(u\) will change given a small change in \(x_1\) and a small change in \(x_2\). If I let \(du\) = 0 (hold utility constant) and solve for \(\frac{dx_2}{dx_1}\) to get the formula for the marginal rate of substitution (drop the negative sign). This is a proof that the MRS can be calculated by the partial derivative of \(u\) with respect to \(x_1\) divided by the partial derivative of \(u\) with respect to \(x_2\):

\[\begin{align} du &= \frac{\partial u}{\partial x_1} dx_1 + \frac{\partial u}{\partial x_2} dx_2\\ 0 &= \frac{\partial u}{\partial x_1} dx_1 + \frac{\partial u}{\partial x_2} dx_2\\ - \frac{\partial u}{\partial x_1} dx_1 &= \frac{\partial u}{\partial x_2} dx_2\\ \frac{d x_2}{d x_1} &= \frac{- \frac{\partial u}{\partial x_1}}{\frac{\partial u}{\partial x_2}}\\ MRS &= \frac{\frac{\partial u}{\partial x_1}}{\frac{\partial u}{\partial x_2}}\\ \end{align}\]

9) Use the formula I derived just above to calculate the marginal rate of substitution (MRS) for \(u(x_1, x_2) = x_1 x_2\).

Answer:

10) Calculate and simplify the MRS for \(u(x_1, x_2) = x_1^{1/3} x_2^{2/3}\).

Answer: